Twijfelen aan de Werkelijkheid (9b)
Dit hoef je absoluut niet te lezen als je slechte herinneringen hebt aan wiskunde.
Cartesisch product; Cartesische coördinaten
Het Cartesisch product van twee verzamelingen \(X\) en \(Y\) is de verzameling van alle paren \((x,y)\) met het eerste lid genomen uit \(X\) en het tweede uit \(Y\).
De truc van de analytische meetkunde is dat je die paren gebruikt om punten in het vlak aan te duiden. Leg over het vlak twee assen die elkaar snijden in een rechte hoek, en die elk de getallenrechte voorstellen. Het paar \((0,0)\) correspondeert dan met het snijpunt van de twee assen. Dit noemen we de oorsprong. En elk punt in het vlak wordt volledig bepaald door een paar \((x,y)\) van zijn \(x\)-coördinaat en zijn \(y\)-coördinaat. Nu kun je algebra gebruiken om meetkunde te doen.
De eenheidscirkel
De Cartesische coördinaten van de eenheidscirkel worden bij voorbeeld gegeven door \(x^2 +y^2 = 1\). De eenheidscirkel heeft de oorsprong \((0,0)\) als middelpunt, en gaat door de punten \((1,0)\), \((0,1)\), \((-1,0)\) en \((0,-1)\). Als je je middelbare school wiskunde bent vergeten: teken een plaatje en je ziet het weer. Of kijk naar het plaatje hieronder.
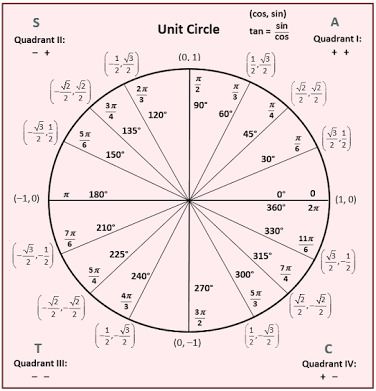
Punten vinden op de eenheidscirkel
Als je de vergelijking \(x^2 +y^2 = 1\) voor de eenheidscirkel eenmaal weet kun je bij voorbeeld de punten op de eenheidscirkel vinden met \(x\)-coördinaat \(\frac{1}{2}\). Of, mooier gezegd, je kunt de snijpunten vinden van de eenheidscirkel met de lijn gegeven door \(x = \frac{1}{2}\). Deze waarde voor \(x\) invullen in de vergelijking voor de eenheidscirkel geeft \(\frac{1}{4} + y^2 = 1\), dat wil zeggen \(y^2 = \frac{3}{4}\), en dus \(y = \pm \sqrt{\frac{3}{4}}\). Daaruit volgen de waarden \(\frac{\sqrt{3}}{2}\) en \(-\frac{\sqrt{3}}{2}\) voor \(y\). De snijpunten zijn dus \((\frac{1}{2},\frac{\sqrt{3}}{2})\) en \((\frac{1}{2},-\frac{\sqrt{3}}{2})\).
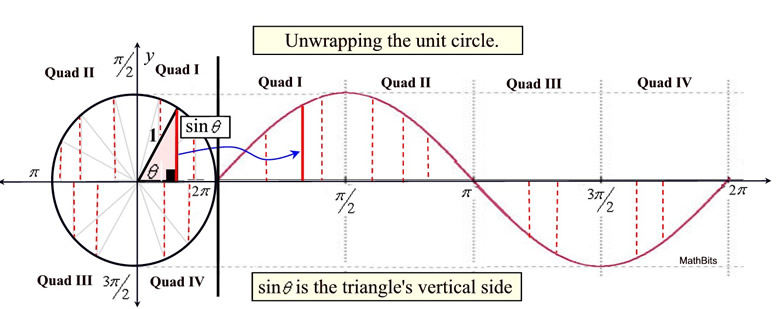
De eenheidscirkel en het gedrag van golven
Je kunt de eenheidscirkel gebruiken om het gedrag van golven te bestuderen. Stel je voor dat je met een punt \(P\) tegen de klok in een rondje draait door de eenheidscirkel, beginnend bij punt \((1,0)\). Dan beschrijft de verandering van de \(y\)-coordinaat tijdens deze beweging de sinus van de hoek \(\theta\) die de lijn door \(P\) en de oorsprong maakt met de positieve \(x\)-as, en de verandering van de \(x\)-coordinaat beschrijft de cosinus van deze hoek. Bij voorbeeld: neem als punt \(P\) het punt \((\frac{1}{2},\frac{\sqrt{3}}{2})\). Dan is de hoek \(\theta\) die de lijn door \(P\) en de oorsprong maakt met de positieve \(x\)-as een hoek van 60 graden. De sinus van een hoek van 60 graden is \(\frac{\sqrt{3}}{2}\) en de cosinus is \(\frac{1}{2}\).