Een wetenschappelijk antwoord op een filosofische vraag
De Koninklijke Zweedse Academie voor Wetenschappen heeft de Nobel prijs voor Natuurkunde voor 2022 toegekend aan Alain Aspect, John F. Clauser en Anton Zeilinger. Hun wetenschappelijke verdienste is dat zij met behulp van natuurkundig experimenteren een filosofisch denkbeeld hebben kunnen weerleggen, namelijk de door Albert Einstein gekoesterde gedachte dat de natuur geen ‘spookachtige’ (spooky) actie op afstand kent.
Volgens de relativiteitstheorie gaat niets in de natuur sneller dan het licht. In een artikel uit 1935 van Einstein samen met Boris Podolsky en Nathan Rosen (samen beroemd geworden als EPR) [1] wordt een gedachtenexperiment voorgesteld dat later bekend werd als de EPR paradox. Hier is een variant. Stel je voor dat je twee deeltjes die kwantumtheoretisch zijn verstrengeld elk een andere kant op stuurt. Elementaire deeltjes hebben een eigenschap die spin heet. De manier waarop je je dat enigszins kunt voorstellen is dat zo’n deeltje razendsnel ronddraait. Leg je rechterhand met uitgestrekte duim om zo’n deeltje, met je vingers in de draairichting. Als je duim dan naar boven wijst is de spin op, als hij naar beneden wijst neer. Je kunt spin in verschillende richtingen meten. De uitkomst van zo’n meting is dan steeds op of neer. Een verstrengeld deeltjespaar kan een spin hebben gelijk aan nul. Dat wil zeggen dat als de spin van het ene deeltje op is, die van het andere deeltje neer moet zijn, en andersom. De vraag is nu: hebben die deeltjes al vanaf het begin een welbepaalde spin, of pas vanaf het moment dat de spin van een van de deeltjes gemeten wordt? Als het laatste het geval was, dan waren ze echt verstrengeld. Volgens Einstein (of EPR) is het antwoord op deze vraag ‘vanaf het begin’, want de werkelijkheid is volgens hem objectief gegeven, dus het kan niet zo wezen dat meten eigenschappen creëert die er daarvoor niet waren, en een meting die hier wordt uitgevoerd kan zeker geen effect heel ergens anders hebben.
Lange tijd werd betwijfeld of dit eigenlijk wel een natuurkundige kwestie was. Was het niet net zo metafysisch als de middeleeuwse vraag hoeveel engelen er kunnen dansen op de punt van een naald? Verrassend genoeg bewees de Noordierse natuurkundige John Stuart Bell in 1964 dat een experimenteel antwoord mogelijk was op de vraag van Einstein/EPR [2]. We kunnen de beroemde stelling van Bell zien als een gedachtenexperiment dat een suggestie doet voor echt experimenteren. Die echte experimenten zijn later uitgevoerd door Aspect, Clauser en Zeilinger, en dat onderzoek uit de vorige eeuw heeft hen de Nobelprijs van 2022 opgeleverd.
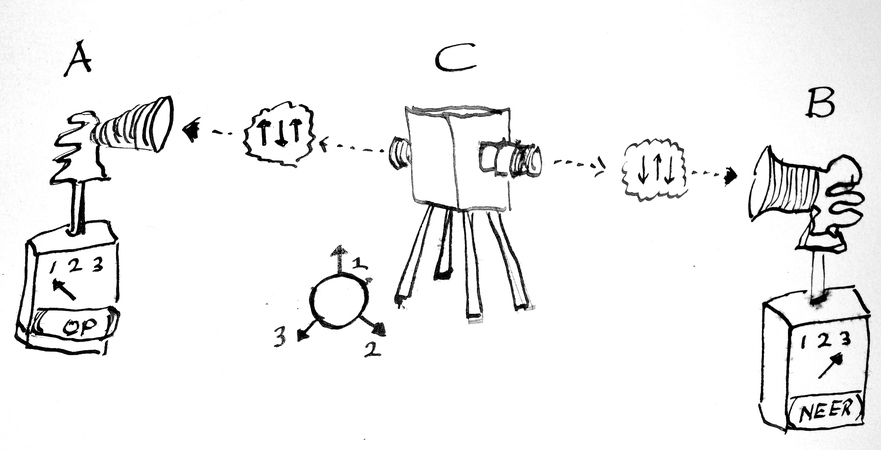
De nu volgende uitleg van het gedachtenexperiment van Bell heb ik te danken aan een briljant artikel van David Mermin [3] waar ik in een video van Brian Greene op werd geattendeerd. Neem een paar verstrengelde deeltjes en twee meetinstrumenten die spin kunnen meten in drie verschillende richtingen. Denk aan drie spaken in een wiel, met hoeken van 120 graden ertussen, zoals op een vredesteken. De uitkomsten van die metingen zijn steeds op of neer. Noem de meetinstrumenten A en B. De meetinstrumenten kunnen in drie toestanden verkeren. In toestand 1 meten ze spin in de eerste richting (0 graden), in toestand 2 in de tweede (120 graden), en in toestand 3 in de derde (240 graden). Een bron C schiet verstrengelde deeltjes af, een deeltje naar A en het andere deeltje naar B. Verstrengeling wil zeggen dat op het moment dat in een van de richtingen spin op wordt gemeten bij het ene deeltje, de spin in dezelfde richting bij het andere deeltje neer moet zijn en andersom. Bij een hoek van 120 graden (één derde van de cirkelboog van 360 graden) in de metingen wordt volgens de kwantummechanica in precies \(1/4\) van de gevallen verschillende spin gemeten.
Stel dat Einstein ongelijk heeft. Dan ‘ontstaat’ de welbepaalde spin van beide deeltjes pas op het moment dat er gemeten wordt, waarbij alle uitkomsten even waarschijnlijk zijn. Stel bij voorbeeld dat in richting 1 bij A op wordt gemeten. We wisselen de meetrichtingen willekeurig af, dus de kans dat bij B in richting 1 wordt gemeten is \(1/3\). De uitkomst van deze meting is neer. De kans dat er bij B in richting 2 wordt gemeten is \(1/3\). De kans dat in deze richting neer wordt gemeten is \(1/4\). De kans dat er bij B in richting 3 wordt gemeten is \(1/3\). Kans op neer in deze richting is \(1/4\). De totale kans op neer bij B is dus \(1/3 + 1/12 + 1/12 = 1/2\). Waar het op neerkomt is dit: als we de toestanden van A en B willekeurig genereren dan zijn de uitkomsten ‘zelfde uitslag’ (allebei op of allebei neer) en ‘verschillende uitslag’ precies even waarschijnlijk.
Maar stel nu eens dat Einstein gelijk heeft, dat wil zeggen, dat deeltjes in alle richtingen die we later gaan meten al een welbepaalde spin hebben vanaf het moment dat de ‘verstrengeling’ plaatsvindt. Dan correspondeert \(\uparrow\downarrow\uparrow\) (spin in de eerste richting op, in de tweede richting neer, in de derde richting op) met \(\downarrow\uparrow\downarrow\) (alle spin richtingen omgekeerd), enzovoorts. Omdat de combinaties \(\uparrow\uparrow\uparrow\) en \(\downarrow\downarrow\downarrow\) niet voorkomen - de spin kan niet in alle drie de richtingen hetzelfde zijn - blijven er zes mogelijke patronen over, steeds met twee pijlen in de ene richting en een pijl in de andere richting. De meetinstrumenten kunnen in drie toestanden verkeren. Dat geeft dus de volgende mogelijke combinaties: \(11, 12, 13, 21, 22, 23, 31, 32, 33\). Hierbij staat bij voorbeeld \(13\) voor: A meet spin in richting 1 en B meet spin in richting 3 (zie de situatie in de tekening hierboven). Als we de standen van A en B steeds willekeurig kiezen zijn al deze combinaties even waarschijnlijk.
Stel dat een deeltje bij A aankomt in de toestand \(\uparrow\downarrow\uparrow\). Ga na dat dan de meetuitslagen verschillend zullen zijn bij de combinaties \(11, 13, 22, 31, 33\), en dat de meetuitslagen hetzelfde zullen zijn bij de andere vier combinaties. Meer in het algemeen geldt: de uitslagen zullen verschillend zijn in de drie gevallen waar A en B in dezelfde toestand zijn en in de twee gevallen waarin A en B in verschillende toestand zijn maar meten in richtingen waarin het deeltje identieke spin heeft; de uitslagen zullen overeenkomen in de vier gevallen waar de toestanden verschillend zijn en meten in richtingen waarin het deeltje verschillende spin heeft. Met andere woorden, hier treedt een asymmetrie op. Als Einstein gelijk heeft moet de situatie van een verschillende uitslag zich voordoen in \(5/9\) van de gevallen, maar volgens de kwantumtheorie zal deze situatie zich voordoen in de helft van de gevallen. In principe kunnen we dus door meten aan de weet komen of Einstein gelijk had.
Door het werk van Aspect, Clauser en Zeilinger weten we nu echt helemaal zeker dat Einstein ongelijk had. Maar wat betekent dit precies? Ten eerste dat wetenschap van nut kan zijn om filosofische vragen te beantwoorden. Ten tweede dat kwantumtheoretische verstrengeling echt bestaat. Ten derde dat de werkelijkheid niet lokaal is: een meting op punt A kan inderdaad in een willekeurig ver weg punt B een onmiddellijk effect hebben, hoe vreemd dit ook klinkt. Dit lijkt op een tegenspraak tussen relativiteitstheorie en kwantumtheorie. Als dit een echt probleem is dan zouden natuurkundigen het scherp moeten kunnen krijgen. Richard Feynman schreef hier in 1982 dit over [4]: ‘It has not yet become obvious to me that there’s no real problem. I cannot define the real problem, therefore I suspect there’s no real problem, but I’m not sure there’s no real problem. So that’s why I like to investigate things.’ Dat lijkt me nog steeds een goede samenvatting van de stand van zaken. Deze wolk van niet weten staat de ontwikkeling van technologie die berust op kwantum verstrengeling (kwantum rekenen, kwantum simulatie, kwantum communicatie) geenszins in de weg, want niemand hoeft meer te twijfelen aan deze kwantumtheoretische werkelijkheid.
[1] A. Einstein, B. Podolsky and N. Rosen, Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?, Physical Review, 47 (777), 1935.
[2] John Stuart Bell, On the Einstein Podolsky Rosen Paradox, Physics 1(3), 1964.
[3] N. David Mermin, Is the moon there when nobody looks? Reality and the quantum theory, Physics Today, 1985.
[4] Richard P. Feynman, Simulating Physics with Computers, International Journal of Theoretical Physics, 21(6/7), 1982.