Twijfelen aan de Werkelijkheid (18)

Je zou deze reeks vanaf het begin kunnen lezen door hier te beginnen. Maar nodig is dat absoluut niet.
De Stelling van Pythagoras
Beschouw het plaatje hierboven. We zien vier rode rechthoekige driehoeken met rechthoekzijden \(a\) en \(b\) en met schuine zijde \(c\). We moeten laten zien dat het kwadraat van de schuine zijde gelijk is aan de som van de kwadraten van de rechthoekzijden.
Welnu. Het grote rode vierkant heeft een zijde met lengte \(a + b\). De oppervlakte van het grote rode vierkant is dus \((a + b)^2\), en uitvermenigvuldigen geeft \(a^2 + 2ab + b^2\). Het witte vierkant binnenin, met een plaatje van hoe Pythagoras er heel misschien zou hebben kunnen uitgezien, heeft oppervlakte \(c^2\). Elk van de rode driehoeken heeft oppervlak \(\frac{1}{2}ab\); die vier driehoeken hebben dus samen oppervlak \(2ab\). Dat kun je trouwens ook zien aan het feit dat ze samen twee rechthoeken vormen met zijden \(a\) en \(b\). Het oppervlak van het grote vierkant wordt dus ook beschreven door \(c^2 + 2ab\). Dit geeft:
\[ a^2 + 2ab + b^2 = c^2 + 2ab. \]
Aan beide kanten \(2ab\) aftrekken geeft: \(a^2 + b^2 = c^2\). Hiermee is de stelling van Pythagoras bewezen.
Maar de algebra is hier eigenlijk overbodig. Het kan ook met twee plaatjes, en dan wordt het een soort Tangram.

Knip de driehoeken uit de plaatjes en zie in dat de oppervlakken die je overhoudt gelijk moeten zijn. QED. QED is een afkorting van Quod Erat Demonstrandum. Dat is Latijn, en het betekent: Dit is wat bewezen moest worden.
Het voorbeeld geeft aan dat je soms dingen kunt bewijzen zonder dat er woorden aan vuil worden gemaakt. Een bewijs is niets meer of minder dan een gestroomlijnde manier om in te zien dat een wiskundige bewering waar is. Als je meer wilt weten over het verband tussen inzien en bewijzen zou het boek Inzien en Bewijzen, van Albert Visser en mij, interessant voor je kunnen zijn.
De afstand tussen punten in een vlak
De stelling van Pythagoras komt in de analyse voortdurend van pas, want deze stelling zegt iets wezenlijks over het begrip afstand. Neem twee willekeurige punten in het platte vlak. Van Descartes weten we dat we die punten kunnen aanduiden met coördinaten \((x,y)\) en \((x',y')\). Met de Stelling van Pythagoras zien we nu dat het kwadraat van de afstand tussen die punten altijd wordt gegeven door:
\[ s^2 = (x - x')^2 + (y - y')^2. \]
Stel nu dat we de oorsprong verplaatsen van (0,0) naar een punt (a,b). Dat heet: een translatie van het vlak. De punten krijgen nu nieuwe coordinaten \((x-a,y-b)\) en \((x'-a,y'-b)\). Opnieuw het kwadraat van de afstand uitrekenen geeft:
\[ ((x-a) - (x' - a))^2 + ((y-b) - (y'-b))^2 = (x - x')^2 + (y - y')^2 = s^2.\]
Wow! Het kwadraat van de afstand verandert niet. Wiskundigen zeggen: afstanden zijn invariant voor translatie.
Ook als we het vlak draaien (een rotatie uitvoeren) verandert (het kwadraat van) de afstand tussen de punten niet. Kijk maar naar dit plaatje.
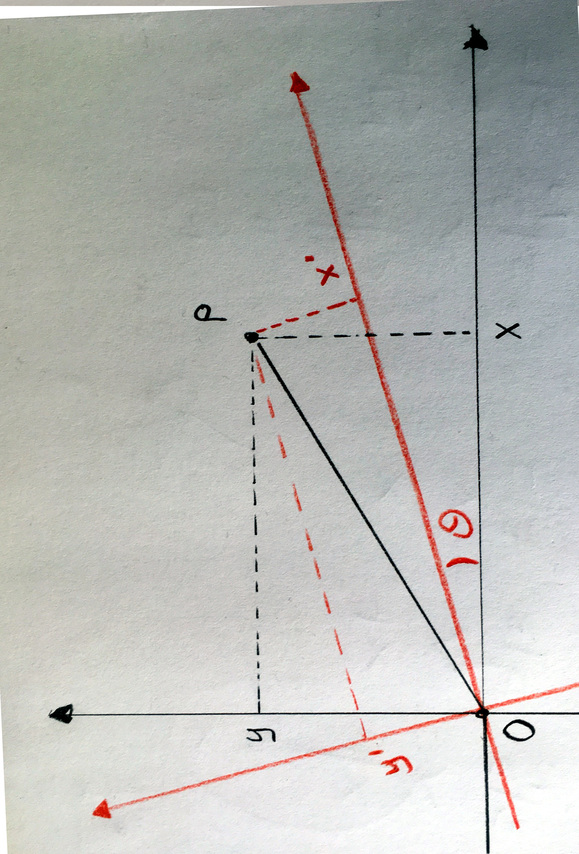
We zien hier een coördinatenstelsel \(xy\) dat over een hoek \(\theta\) om de oorsprong gedraaid is, tegen de wijzers van de klok in. Dit heet een rotatie om de oorsprong. Het geeft een nieuw stelsel \(x'y'\). Beschouw het lijnstuk \(OP\) tussen de oorsprong en het punt \(P\). Volgens Pythagoras is het kwadraat van de lengte van dit lijnstuk gelijk aan \(x^2 + y^2\). Maar dit is ook gelijk aan \(x'^2 + y'^2\). Kijk maar in het plaatje. Wiskundigen zeggen: afstanden zijn invariant voor rotatie.
Afstand tussen punten in de ruimte
We zien dus dat de Stelling van Pythagoras ons iets vertelt over het begrip afstand. Het is dan ook niet verwonderlijk dat de stelling ook geldt in de drie-dimensionale ruimte. Een punt in de ruimte wordt, weer met dank aan Descartes, aangeduid als een drietal coördinaten \((x,y,z)\). Het kwadraat van de afstand tussen twee punten \((x,y,z)\) en \((x',y',z')\) in de ruimte wordt nu gegeven door:
\[ s^2 = (x - x')^2 + (y - y')^2 + (z - z')^2. \]
Net als in het platte vlak zijn afstanden in de ruimte invariant voor translatie en rotatie. Je kunt deze invarianties zien als eigenschappen van de ruimte, of eigenschappen van het begrip afstand. En een vraag die je jezelf zou kunnen stellen is deze:
Als we het hebben over afstanden in de ruimte, hebben we het dan over iets in de werkelijkheid of over iets in onze geest?
Dit is een zeer wezenlijke vraag. Zij is door allerlei filosofen en beoefenaars van de natuurwetenschap verschillend beantwoord. Pythagoras zou ongetwijfeld hebben gezegd: over de werkelijkheid. En daarbij zouden we dan moeten aantekenen dat voor hem getallen de essentie van de werkelijkheid uitmaken.
Iets om zelf over na te denken: is de driedimensionale ruimte waar wiskundigen als Pythagoras en Euclides en Descartes het over hebben iets in de werkelijkheid? Of is het iets dat alleen bestaat in onze geest? En wat is eigenlijk het verschil tussen ‘werkelijk bestaan’ en ‘in onze geest bestaan’?
Galileo over invarianties
Galileo Galilei (1564 – 1642) verdedigde het principe van de relativiteit in de natuur. Hij bestudeerde coördinatenstelsels die ten opzichte van elkaar in beweging waren en stelde dat we in de natuur geen vaste punten hoeven aan te nemen. Als twee objecten ten opzichte van elkaar bewegen met uniforme snelheid - natuurkundigen zeggen: eenparig rechtlijnig - dan maakt het niet uit of we aannemen dat het eerste object stilstaat en het tweede beweegt of andersom.
Zijn voorbeeld is een schip dat beweegt ten opzichte van de kade. We kunnen de natuur beschrijven vanaf een standpunt op de kade maar ook vanaf een standpunt op het schip. En dan zien we dat alles op het schip gebeurt precies zoals het op de kade gebeurt. Als je een steentje laat vallen op het bewegende schip dan valt het recht naar beneden ten opzichte van het schip en niet ten opzichte van de kade. Dit bewijst volgens Galileo dat Aristoteles ongelijk had met zijn opvattingen over beweging.
Aristoteles’ theorie van beweging is lastig uit te leggen, want de Griekse filosoof verklaart beweging uit de aard der dingen: zware dingen hebben de aard om naar beneden te bewegen, lichte dingen juist de aard om naar boven te gaan. Uit die opvatting volgt dat objecten sneller vallen naarmate ze zwaarder zijn. Volgens Galileo was de hele manier van denken verkeerd, en hij verzon zijn beroemde val-experimenten om Aristoteles’ theorie te weerleggen.
Galileo’s beroemde Dialoog over de twee belangrijkste wereldsystemen (1632) zit vol met overtuigende gedachtenexperimenten. Als je op een schip zit dat langzaam met constante snelheid vaart door een rustig kanaal dan merk je pas dat je beweegt door naar buiten te kijken. Wij kennen dit van naast elkaar stilstaande treinen op Utrecht Centraal. Je zit in de trein, kijkt uit het raampje, en je ziet beweging ten opzichte van de trein naast je. En je weet niet meteen of het jouw trein is die vertrekt of de andere trein.
Voor een beweging met constante hoeksnelheid - de beweging van de aarde om haar as - geldt deze invariantie overigens niet. In feite kun je de beweging van de aarde voelen als je op een warme zomernacht in Frankrijk naar de sterren zit te kijken vanuit een heel gemakkelijke leunstoel, met een flesje armagnac binnen handbereik. Als je maar lang genoeg blijft zitten staren voel je na een tijdje jezelf bewegen ten opzichte van de sterren. Althans zo gaat het met mij, maar dat kan dan natuurlijk ook komen door de armagnac.
Maar serieuzer, de beweging van de aarde om haar as veroorzaakt de Coriolis-kracht die ervoor zorgt dat tropische stormen op het Noordelijk Halfrond met de klok mee draaien en op het Zuidelijk Halfrond tegen de klok in. In de tijd van Galileo was dit overigens nog niet bekend, want op kleine schaal merk je die kracht niet. Het feit dat je de beweging van de aarde niet kon voelen werd juist ingebracht als tegenwerping tegen het heliocentrische wereldbeeld dat door Copernicus en Galileo werd geopperd. De tegenwerpers waren de Jezuïeten die Galileo bestreden, en misschien dronken die niet genoeg armagnac.
Beweging veronderstelt een tijdscoördinaat. Neem een gebeurtenis die zich op tijdstip \(t\) voordoet op plaats \((x,y,z)\) in de ruimte volgens coordinatenstelsel \(C\). De gebeurtenis zou kunnen zijn dat Jan zichzelf een glaasje armagnac inschenkt. Noteer dit als \((x,y,z,t)\). Dan wijst \((x,y,z)\) naar het lieu dit (gehucht) Lavidalle in Frankrijk en \(t\) naar een bepaald tijdstip op een bepaalde datum. Beschouw nu een coördinatenstelsel \(C'\) met dezelfde as-richtingen dat met snelheid \(v\) beweegt langs de \(x\)-as, zó dat op tijdstip \(0\) de oorsprong van \(C\) samenvalt met de oorsprong van \(C'\). Dan heeft de gebeurtenis vanuit \(C'\) gezien de coördinaten \((x',y',z',t')\). Bovendien geldt dat \(x' = x - vt\), \(y = y'\), \(z = z'\) en \(t = t'\). Merk op dat het voor het verloop van de tijd niet uitmaakt hoe je naar het gebeuren kijkt. De tijd is voor Galileo Galilei - en iets later, voor Isaac Newton - nog steeds absoluut.
Pythagoras voor ruimtetijd?
Albert Einstein (1879 – 1955) behoort met Galileo Galilei en Isaac Newton (1642 – 1727) tot de grootste natuurkundigen aller tijden. Daarom is het verrassend dat de essentie van zijn speciale relativiteitstheorie, waar Einstein in 1905 in één klap wereldberoemd mee werd, eenvoudig valt uit te leggen, en … dat er een rechtstreeks verband blijkt te zijn met de stelling van Pythagoras.
Relativiteit in de zin van Einstein’s theorie kunnen we zien - ik heb dit perspectief te danken aan de Amerikaanse astrofysicus Richard Conn Henry (1940) - als het gevolg van het generaliseren van de stelling van Pythagoras naar tijd als vierde dimensie.
Hierboven hebben we al kennisgemaakt met coördinaten \((x,y,z,t)\) om een gebeurtenis op tijdstip \(t\) op plaats \((x,y,z)\) aan te duiden. Maar bestaat er ook een begrip afstand - zoals we gezien hebben het begrip waar Pythagoras’ stelling om draait - voor ruimtetijd?
Simpel generaliseren tot
\[ s^2 = (x - x')^2 + (y - y')^2 + (z - z')^2 + (t - t')^2. \]
gaat niet werken, want daarmee behandel je tijd als een vierde ruimte-coördinaat, en tijd gedraagt zich anders. Bovendien hebben we wat natuurkundigen een dimensie-probleem noemen: afstand druk je uit in meters, tijd is seconden, en meters en seconden kun je niet zomaar bij elkaar optellen.
De Gegeneraliseerde Stelling van Pythagoras
Wat - wonder boven wonder - wel blijkt te werken is een generalisering waarbij het laatste plusteken verandert in een minteken. Dit geeft de kern van Einstein’s speciale relativiteitstheorie, in de herformulering van Hermann Minkowski (1864 – 1909). Minkowski was de vroegere leermeester van Einstein die in 1907 een elegante meetkundige herformulering gaf van Einsteins theorie uit 1905.
\[ s^2 = (x - x')^2 + (y - y')^2 + (z - z')^2 - (t - t')^2.\]
Wikipedia is je vriend, dus lees daar verder over Minkowski space. Let op: onze regel geeft het kwadraat van ruimtetijd afstand terwijl Minkowski’s regel is geformuleerd in termen van afstand. Vandaar dat de vierkantswortel uit \(-1\), het complexe getal \(i\), in zijn formulering figureert. Maar daar hoeven we ons hier niet druk om te maken.
Om de dimensies goed te krijgen moeten we alleen nog tijd converteren naar afstand. Hoe converteren we seconden in meters? Door te vermenigvuldigen met de lichtsnelheid.
Als we de lichtsnelheid stellen op een lichtseconde per seconde, dan maakt dit de lichtsnelheid gelijk aan \(1\), en dan is er verder geen aanpassing nodig. Dit voorstel van de wiskundige Henri Poincaré (1854 – 1912) is elegant, maar heeft het nadeel dat we dan afstand moeten gaan meten in lichtseconden in plaats van in meters, en dat is op aarde niet praktisch. Als we de lichtsnelheid in meters per seconde willen uitdrukken, dan moeten we converteren met behulp van \(c = 299.792.458\) meter per seconde. Dit geeft de volgende Gegeneraliseerde Stelling van Pythagoras voor de gekwadrateerde afstand tussen twee punten \((x,y,z,t)\) en \((x',y',z',t')\) in ruimtetijd.
\[ s^2 = (x - x')^2 + (y - y')^2 + (z - z')^2 - c^2(t - t')^2\]
Als we hiermee gaan rekenen zullen we merkwaardige dingen zien gebeuren.
Nog even over de lichtsnelheid
De lichtsnelheid, heeft iemand die gemeten? Hoe dan? Merkwaardig genoeg blijkt
\(c = 299.792.458\) meter per seconde
een definitie te zijn, want mensen die denken dat één meter de lengte is van een staaf platina die in Parijs wordt bewaard hebben even niet opgelet. In 1983 is één meter geherdefinieerd als “de afstand die licht in vacuum aflegt gedurende fractie \(1/299.792.458\) van een seconde”. Deze definitie illustreert dat als we de seconde als eenheid van tijd hebben vastgelegd, daarmee in feite ook een eenheid van lengte is vastgelegd: de lichtseconde.
Maar er is eerst echt gemeten, toen die platina staaf in Parijs nog serieus werd genomen. Op allerlei manieren zelfs, kijk maar op Wikipedia, waar witte mannen met een opleiding zitten te popelen om het allemaal aan ons uit te leggen. We kunnen het trouwens ook zelf uitrekenen. Alle electromagnetische straling beweegt zich met de snelheid van het licht. Een huishoudmagnetron gebruikt straling met een frequentie van 2,45 gigahertz en een golflengte van 12,2 centimeter (opgezocht op internet). Omrekenen naar hertz en meters: 2,45 gigahertz is 2.450.000.000 hertz (trillingen per seconde) en 12,2 centimeter is 0,122 meter. Het product van die twee is bij benadering de lichtsnelheid, want de snelheid van de golven, in meters per seconde, is het product van het aantal golven per seconde en de golflengte in meters. Dat geeft 298.900.000 meter per seconde. Een beetje minder dan de waarde voor de lichtsnelheid die hierboven is vermeld, want de magnetronruimte is geen vacuum.
Weer kunnen we de filosofische vraag stellen: hebben we het nu over de werkelijkheid of over iets in onze geest? We zouden kunnen zeggen dat de speciale relativiteitstheorie een model is, bedoeld om een aspect van de werkelijkheid adekwaat te beschrijven. Of de modellering geslaagd is moet blijken uit waarnemingen. De speciale relativiteitstheorie voorspelde bij voorbeeld dat de aanname van een ether substantie waarin lichtgolven bewegen overbodig is, en dat de lichtsnelheid in vacuum vanuit het standpunt van elke waarnemer hetzelfde is, hoe die waarnemers ook ten opzichte van elkaar bewegen. Die voorspellingen bleken te kloppen met observaties. Als een model niet in tegenspraak is met hoe de werkelijkheid zich aan ons toont zegt dat iets over de bruikbaarheid ervan. En misschien, heel misschien, ook iets over de aard van de werkelijkheid.
Alle miljardairs naar Mars
Volgende keer doen we misschien een gedachtenexperiment. We zouden kunnen kijken wat er gebeurt als we alle miljardairs in een ruimteschip naar Mars schieten, laten we zeggen met de helft van de lichtsnelheid, en met Elon Musk als expeditieleider.