Twijfelen aan de Werkelijkheid (17)

Deze reeks begint hier, dus je zou vanaf het begin kunnen lezen. Voor goed begrip van wat volgt is dat echter absoluut niet nodig.
Het wonder van wiskunde
Hoe kunnen we dingen ooit zeker weten? Hoe kunnen we op een precieze manier praten over dingen? Aan welke eisen moet onze taal voldoen om te kunnen praten over heel, heel simpele zaken? Een simpele zaak - zo lijkt het - is het tellen en rekenen met getallen
\[0, 1, 2, 3, \]
enzovoorts. Wiskundigen noemen dit de natuurlijke getallen. Die getallen bestaan op een bepaalde manier echt. Er bestaat kennelijk een getallen-werkelijkheid. En deze getallen hebben eigenschappen: even of oneven, deelbaar door drie of niet, priemgetal of niet, enzovoort. Je kunt over deze zaken nadenken. Met behulp van wiskunde kunnen we diepe waarheden over deze getal-dingen aan de weet komen.
Logica en de aard van wiskundig denken
Logica is een poging om dit proces van inzicht krijgen in de getallen-werkelijkheid te begrijpen. Logica kijkt naar de eigenschappen van de taal die we gebruiken om te praten over wiskundige zaken. Logica bestudeert de kleinste stapjes die zorgen voor de stevigheid en de structuur van wiskundige bewijzen. Verrassend genoeg hebben logici ons laten zien dat er grenzen zijn aan wat we kunnen zeggen wanneer we een bepaalde taal gebruiken.
Aanvankelijk besloeg het terrein van logisch redeneren ons denken van alledag. Toen het vak logica ontstond was het nauw verbonden met rhetorica en filosofie, en stond het ver af van wiskunde. Pas veel later raakten logici geïnteresseerd in de aard van wiskundig denken. Hoe is het mogelijk dat wiskundig denken zo solide is? Wat is de aard van het proces van wiskundige bewijzen construeren en bewijzen verifiëren?
Wat is eigenlijk een bewijs? Wat zijn de eigenschappen van de taal waarin we bewijzen opschrijven? Is er een methode om bewijzen te vinden, of misschien zelfs een nog onontdekte hoofdsleutel die de wereld van de wiskundige waarheden voor ons opent? Zo’n magische sleutel is nog door niemand gevonden. Vrijwel niemand gelooft dat dat ooit zal gebeuren, maar we hebben aan de andere kant geen bewijs dat zo’n sleutel niet kan bestaan. Deze ietwat genante situatie houdt verband met het beroemde onopgeloste P versus NP probleem.
De vraag naar de vierkantswortel van 2
Laten we, om te zien waar logica over gaat, eens kijken naar een wiskundige vraag. Wat is de lengte \(x\) van de diagonaal van een vierkant met zijden van lengte 1?
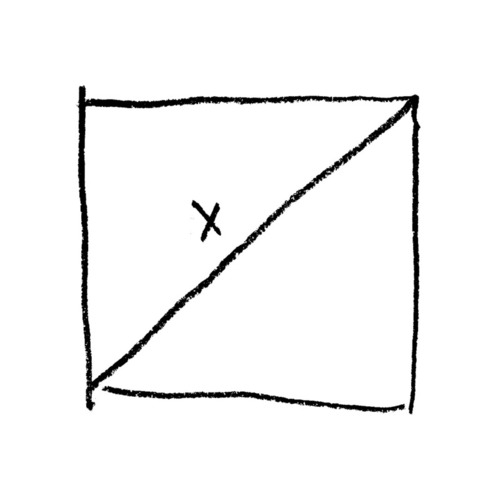
We kunnen iets over \(x\) aan de weet komen door vier van zulke vierkanten bij elkaar te leggen:
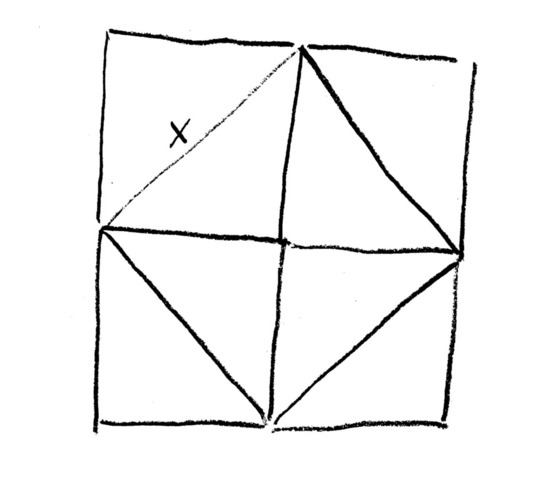
Als vierkanten zijden hebben met lengte \(1\), dan moet het oppervlak van het mozaiek van vier vierkanten gelijk zijn aan \(4\). En het oppervlak van het gearceerde deel is precies de helft hiervan, dus dat oppervlak moet grootte \(2\) hebben:
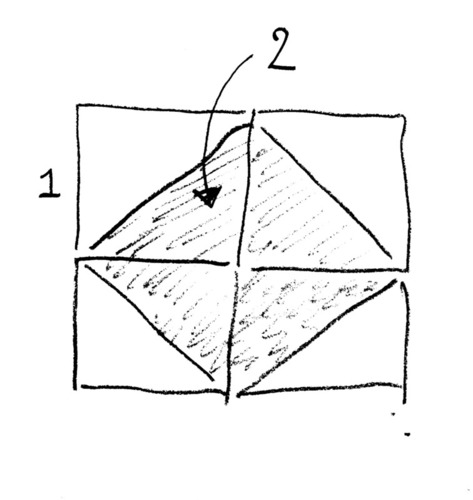
Daarmee weten we iets over \(x\). Het product van \(x\) met zichzelf, ofwel het kwadraat van \(x\), moet \(2\) bedragen. Wat zegt dat over \(x\)? Hoe vinden we de grootte van \(x\)?
Terug naar Babylon
Stel je nu voor dat je een heel slim jongetje of meisje bent, en projecteer jezelf terug in de tijd. Je bent nu in het oude Babylonië. Verderop is de beroemde toren in aanbouw, maar jij hebt geen tijd om daar op te letten want jij zit met deze vraag. We weten dat iemand zoals jij het antwoord moet hebben gevonden. Dit kleitablet is het bewijs:

Op dit tablet staat een getal gekerfd bij een van de zijden van het vierkant, en ook bij de diagonaal van het vierkant staat een getal. Het blijkt dat het getal bij de diagonaal bijzonder weinig verschilt van de vierkantswortel van \(2\) maal het getal bij de zijde van het vierkant. De Babyloniërs moeten dus een manier hebben gevonden om - bij benadering - de vierkantswortel van \(2\) te berekenen. Hoe hebben ze dat geflikt?
Om deze prestatie naar waarde te schatten zou je jezelf kunnen afvragen: hoe zou ik dit zelf hebben aangepakt? Wiskunde zoals het op school wordt onderwezen is vaak gortdroog. Een manier om er leven in te blazen is: wiskunde bedrijven vanuit de eerste persoon. De eerste persoon ben jij zelf. De vraag wordt dus: hoe zou ik dit aanpakken, als ik alleen gebruik zou mogen maken van wat de Babyloniërs konden weten?
De Babylonische methode
Je weet dus waar je op uit bent. Je wilt een getal \(x\) vinden dat als je het met zichzelf vermenigvuldigt de uitkomst \(2\) geeft. Je weet dat \(x\) groter moet zijn dan \(1\), want dat vertelt het plaatje je al. We zien dan dat \(1\) een onderschatting is van de gezochte uitkomst.
Hier is het inzicht dat dit slimme jongetje of meisje onder de schaduw van de toren van Babel moet hebben gehad. Als we een onderschatting (overschatting) \(m/n\) hebben van \(x\), dan is \(2n/m\) een overschatting (onderschatting). Om te zien waarom dat zo is moeten we bedenken dat voor \(x\) geldt dat \(\frac{2}{x} = x\). Dit volgt immers direct uit het feit dat het kwadraat van \(x\) gelijk is aan \(2\).
Stel dus dat \(m/n\) een onderschatting is van \(x\), dat wil zeggen, \(m/n < x\). Hieruit volgt dat \(n/m > 1/x\), en dus dat \(2n/m > 2/x = x\). Net zo volgt uit de aanname dat \(m/n\) een overschatting is van \(x\) dat \(2n/m\) een onderschatting is van \(x\).
Als je een onderschatting en een overschatting van \(x\) hebt, dan is het gemiddelde, \(\frac{m/n + 2n/m}{2}\), een betere benadering. Starten met de onderschatting \(1\) geeft overschatting \(2\). Neem het gemiddelde. Dat is \(3/2\). Zie dit als nieuwe benadering. Zie in dat er geen reden is om hier te stoppen.
We willen dichterbij. Het gemiddelde van \(3/2\) en \(4/3\) is \((9/6 + 8/6)/2 = 17/12\). Dat is nog een kleine overschatting, want het kwadraat van \(17/12\) is \(289/144\), dat wil zeggen \(2 + 1/144\). Maar dan is \(24/17\) een onderschatting, en dan kunnen we weer het gemiddelde nemen.
Dat geeft \(577/408\). Hier ergens moeten de Babyloniërs in de problemen zijn geraakt, want je hebt nogal wat klad-kleitablet nodig om verder te kunnen rekenen. Maar we zitten er nu behoorlijk dichtbij, want het kwadraat van \(577/408\) is \(332929/166464\), en dat is gelijk aan \(2 + 1/166464\).
Zou het ook helemaal precies kunnen?
De procedure die ik hier heb beschreven is een heel vroeg en heel slim voorbeeld van wat we tegenwoordig een algoritme noemen. Een rekenmachine die de wortel uit \(2\) uitrekent voert een klein programmaatje uit dat de stappen hierboven een aantal malen doorloopt en dan een benadering uitprint in decimale notatie.
Praktisch gezien is ons probleem opgelost. Maar we kunnen nu een fundamentele vraag stellen, een vraag van het soort waar mijn collega’s op het CWI, tussen wie ik het grootste deel van mijn werkzame leven heb doorgebracht, dag in dag uit mee bezig zijn. De vraag is deze. Stel dat we genoeg tijd zouden hebben, en genoeg klad-kleitablet, of genoeg kladpapier, of genoeg computerkracht, zou het Babylonische algoritme om de vierkantswortel van \(2\) te berekenen - of om het even welk algoritme dat probeert de vierkantswortel van \(2\) uit te drukken als een breuk - ooit een precies antwoord opleveren?
Eureka: een wiskundig bewijs
Hoe moet je zo’n vraag aanpakken? Voor zover we weten hebben de Babyloniërs nooit het antwoord gevonden. Maar de Grieken, uitvinders van de methode van het wiskundig bewijs, hebben de vraag beantwoord. Preciezer gezegd, iemand die lid was van de mysterieschool van Pythagoras kwam erachter. Pythagoras van Samos (ongeveer 570 tot ongeveer 495 v Chr) is een sleutelfiguur voor filosofie en wiskunde, dus ik hoop nog op hem terug te komen. Hoe dan ook, de legende zegt dat het antwoord dat de Pythagoreërs vonden zo’n schok betekende dat ze besloten het geheim te houden. Deze kennis was alleen voor ingewijden in de school. En volgens weer een andere legende heeft er toen iemand, Hippasus van Metapontum geheten, uit de mysterieschool geklapt en is hij daarna vermoord wegens dit hoogverraad.
Het bewijs dat de vierkantswortel van \(2\) niet kan worden uitgedrukt als een verhouding tussen twee natuurlijke getallen \(m\) en \(n\) gaat als volgt. We gaan een tegenspraak afleiden uit de aanname dat dit wel kan. Stel dus dat er natuurlijke getallen \(m\) en \(n\) zijn met de eigenschap dat het kwadraat van \(m\) gedeeld door het kwadraat van \(n\) gelijk is aan \(2\). Dat wil zeggen, we nemen aan dat de Babylonische methode of een andere methode ons een precieze breuk \(m/n\) heeft opgeleverd met de eigenschap dat \(\frac{m^2}{n^2} = 2\), en we gaan uitleggen hoe die aanname ons in logische problemen brengt. En daaruit concluderen we vervolgens dat onze aanname fout was.
Gordels vast, daar gaan we. We mogen aannemen dat \(m/n\) in eenvoudigste vorm is. Meer in het bijzonder nemen we aan dat \(m\) en \(n\) niet allebei even zijn, want als dat zo zou zijn zouden we de breuk kunnen vereenvoudigen door teller \(m\) en noemer \(n\) allebei door \(2\) te delen.
Uit \(\frac{m^2}{n^2} = 2\) volgt dat \(m^2 = 2n^2\). Dit wil zeggen dat \(m^2\) even is. Maar als het kwadraat van een getal even is moet dat getal zelf ook even zijn. Immers, het kwadraat van een oneven getal, zeg \(m = 2p + 1\) is altijd oneven, want we hebben dan \(m^2 = (2p + 1)^2 = 4p^2 + 4p + 1\), dat wil zeggen \(m^2\) is ook oneven. Dus oneven getallen hebben altijd oneven kwadraten. Omdat het kwadraat van \(m\) even is moet \(m\) dus zelf even zijn.
Omdat \(m\) even is is er een natuurlijk getal \(q\) zo dat \(m = 2q\). Dit kunnen we gebruiken om \(m^2 = 2n^2\) te herschrijven als \(4q^2 = 2n^2\). Beide zijden door \(2\) delen geeft \(2q^2 = n^2\). Maar dat is een ramp, want het betekent dat het kwadraat van \(n\) ook even is, en dat \(n\) dus ook even moet zijn. We hebben een tegenspraak afgeleid met de aanname dat \(m\) en \(n\) niet allebei even zijn.
Hieruit volgt dat er geen natuurlijke getallen \(m\) en \(n\) kunnen zijn met de eigenschap dat \(\frac{m^2}{n^2} = 2\). En dat betekent dat de Babylonische methode die steeds betere benaderingen \(m/n\) van de vierkantwortel van \(2\) vindt nooit zal termineren met een precies antwoord.
Verder spelen
Het verhaal van de vierkantswortel van 2 gaat hier verder. Op de computer kun je gemakkelijk de Babylonische methode programmeren. Hier is een Haskell programma dat breuken berekent die dichter en dichter bij de vierkantswortel van \(2\) komen:
bab :: (Integer,Integer) -> (Integer,Integer)
bab (m,n) = (m^2 + 2*(n^2), 2*m*n)
gen :: (a -> a) -> a -> [a]
gen f x = x : gen f (f x)
babseq :: [(Integer,Integer)]
babseq = gen bab (1,1)Uitleg: als \(m/n\) een overschatting (onderschatting) is, dan is \(2n/m\) een onderschatting (overschatting). Het gemiddelde is dan \(\frac{m/n + 2n/m}{2}\). Teller en noemer met \(mn\) vermenigvuldigen geeft \(\frac{m^2 + 2n^2}{2mn}\). Dit verklaart de definitie van bab. De rest van het programma bestaat uit Haskell trucjes om een oneindige lijst van benaderingen te genereren. Wie daar meer over wil weten zou hier eens kunnen kijken.
Als je babseq uitvoert krijg je een eindeloze reeks van paren \((m,n)\) van gehele getallen zo dat hun ratio (dat wil zeggen, hun breuk) steeds dichter bij de vierkantswortel van twee komt.
\[ \frac{1}{1}, \frac{3}{2}, \frac{17}{12}, \frac{577}{408}, \frac{665857}{470832}, \frac{886731088897}{627013566048}, \frac{1572584048032918633353217}{1111984844349868137938112}, \]
\[ \frac{4946041176255201878775086487573351061418968498177}{3497379255757941172020851852070562919437964212608}, \ldots \]
Wow, dit loopt snel op. En dit komt razendsnel dichterbij de precieze uitkomst. En toch, als je het bewijs hierboven begrepen hebt weet je waarom dit proces van benaderen eindeloos moet doorgaan.
De school van Pythagoras
De filosofie-school van Pythagoras was wat we nu een sekte zouden noemen, met Pythagoras als goeroe. De school hield het midden tussen een klooster en een commune. De Pythagoreërs geloofden in zielsverhuizing (reïncarnatie), aten vegetarisch, en gaven vrouwen toegang tot hun gemeenschap. Binnen de school was alle bezit gemeenschappelijk. Een soort Wild, Wild Country dus, maar dan zonder dat het compleet uit de hand liep. En dat kleine dingetje met Hippasus dan? Nu ja, had die eikel zijn mond ook maar moeten houden.
Het kernstuk van de filosofie van de Pythagoreërs was dat de werkelijkheid op het diepste niveau gebaseerd is op wiskunde, en dat het wezen van de natuur bestaat uit mooie verhoudingen tussen getallen. De Pythagoreërs hadden bij voorbeeld ontdekt dat harmonische samenklanken in de muziek te maken hebben met getalsverhoudingen. Als een strakgespannen snaar van een lier wordt verdeeld in stukken die zich verhouden als 1:2 of 2:3 of 3:4 of 4:5, dan zijn de tonen die je krijgt door die twee snaarstukken te tokkelen of aan te strijken in samenklank met elkaar en klinkt er een harmonisch interval (bij 1:2 een octaaf, bij 2:3 een kwint, bij 3:4 een kwart, bij 4:5 een grote terts, bij 5:6 een kleine terts).
Dit komt omdat bij dezelfde snaardikte en snaarspanning een twee keer zo lange snaar twee keer zo langzaam trilt, maar dat wisten de Grieken nog niet. De snaarverhoudingen \(a:b\) corresponderen dus met verhoudingen van trillingsfrequenties \(b:a\). Stapelingen geven harmonische drieklanken. Zo levert de frequentieverhouding 4:5:6 een grote terts akkoord op. De buitenste twee tonen staan in verhouding 4:6 of 2:3, dus ze vormen een kwint, de laagste twee vormen samen een grote terts, en de hoogste twee vormen samen een kleine terts. Voor Pythagoras en zijn leerlingen, die deze verhoudingen ontdekten, illustreerde dit dat de kosmos geordend is door eenvoudige getalsverhoudingen. Alle mooie verhoudingen zijn eenvoudige breuken.
Bestaat er een filosofische methode?
De ontdekking dat de verhouding tussen de diagonaal en de zijde van een vierkant geen breuk was haalde een dikke vette streep door een filosofisch idee over de ordening van de kosmos. Dit illustreert dat wiskunde (en wetenschap in het algemeen) relevant is voor de filosofie. Kennelijk kan wiskunde filosofie onderuit halen.
Wiskundig denken geeft ons toegang tot de wiskundige werkelijkheid, en wiskundige bewijzen geven ons absolute zekerheid. Dit is een wonder. En het feit dat wiskunde ons suggesties kan geven voor hoe de werkelijkheid in elkaar zit is een nog veel groter wonder. Maar is er ook een filosofische werkelijkheid? En is er een filosofische methode die ons betrouwbare antwoorden geeft op filosofische vragen? Of zijn we veroordeeld tot eeuwige filosofische twijfel aan de werkelijkheid?