Twijfelen aan de Werkelijkheid (10)
Lezen vanaf het begin? Zie hier.
Loopt het een beetje, die cursus?
Hoeveel lezers heb ik eigenlijk voor mijn filosofische mini-feuilleton? Vanochtend hadden we het er even over aan de ontbijttafel. Nu ja, idioot veel respons is er niet. Af en toe een complimentje van een fb vriend, daar moet ik het mee doen. Ik kan proberen mezelf wijs te maken dat ik voor een kleine zelfbenoemde elite schrijf, lezers van NRC en de Correspondent en de Groene Amsterdammer, dat soort volk. Ons soort mensen, zeg maar.
Maar volgens Heleen doe ik misschien toch iets fout. Is het handig om het in een eerste alinea al te hebben over het verschil tussen Cartesisch en Cartesiaans? Boeit dat de mensen? Zitten de lezers daar op te wachten? Grijpt dat de aandacht? Maakt het dat men met rode oren de rest van het verhaal gaan lezen? Deze vragen stellen is ze beantwoorden.
Hoe moet het dan? Is het misschien beter om te beginnen over het getwijfel van Marc Rutte en het RIVM? Of over de twijfelachtigheid van Willem Engel? En dan vlak daarna een scherpe draai maken naar twijfel als filosofisch probleem?
Wiskunde, schrikt dat niet af?
En die uitstapjes naar de wiskunde van Descartes, voor wie zijn die eigenlijk bedoeld? Is dat ergens voor nodig? Hmm, goede vraag. Nu ja, ik had net uitgevogeld hoe ik mijn Hakyll systeem moest inrichten om wiskunde notatie te kunnen gebruiken. Dat wilde ik even uitproberen. En het is toch niet verkeerd als mensen bereid zijn een beetje formeel te leren denken? Wiskunde is nu eenmaal de kunde van het formeel denken bij uitstek.
Is het toeval dat Plato, Aristoteles, Descartes, Leibniz, Spinoza uitstekend op de hoogte waren van de wiskunde van hun tijd? Descartes en Leibniz waren zelf vooraanstaande wiskundigen. Of dichter bij onze tijd: Bertrand Russell en Alfred North Whitehead waren allebei zowel wiskundige als filosoof. Whitehead laat zich ergens in zijn geschriften ontvallen dat hij de Duitse continentale traditie in de filosofie liever overslaat, omdat daar gefilosofeerd wordt zonder dat men wiskundig en natuurkundig onderlegd is. Zo, dat kunnen de liefhebbers van Hegel, Nietzsche en Heidegger in hun zak steken.
Over het verschil tussen twijfel en onzekerheid.
Twijfel is: niet weten wat je het best kunt doen in een gegeven situatie. Onzekerheid is: niet precies weten wat de kans is dat een bepaalde situatie zich voordoet. Of om nog even terug te komen op het voorbeeld met de eieren van Savage, twijfel is niet weten wat je met dat laatste ei gaat doen, en onzekerheid is niet weten wat de kans is dat je laatste ei rot is. Uiteraard hebben twijfel en onzekerheid iets met elkaar te maken. En dus is het goed om iets te leren over redeneren met onzekerheid.
Neem het voorbeeld van de PCR test voor corona. Je hebt al een paar dagen een hoestje en een neusverkoudheid, en je twijfelt of je misschien corona hebt. Je besluit je te laten testen. Hoeveel zekerheid geeft die test?
Betrouwbaarheid van de PCR test voor covid-19
Informatie over de betrouwbaarheid van de PCR test voor covid-19 is online te vinden. Maar we moeten een beetje oppassen, want er circuleert hierover desinformatie die door twijfelzaaiers als Pierre Capel en Pieter Borger wordt verspreid. Bij deze lieden kunnen we dus beter niet te rade gaan. Voor betrouwbare informatie over de betrouwbaarheid van de PCR test moeten we ons licht opsteken bij onze kwaliteits-journalistiek. Bij voorbeeld in dit artikel van Lotte van Rosmalen voor Argos. Heerlijk hoor, al die goede journalisten die we hebben.
Een goede test is gevoelig en specifiek
Een perfecte covid-19 test zou precies de mensen eruit pikken die de ziekte hebben. Maar geen enkele test is perfect. We willen dat een test zowel gevoelig is als specifiek. Een gevoelige test geeft weinig fout negatieve uitslagen. Dat wil zeggen, bij een gevoelige test komt het weinig voor dat iemand die de ziekte wel heeft toch een negatieve testuitslag krijgt. Een specifieke test geeft weinig fout positieve uitslagen. Dat wil zeggen: bij een specifieke test komt het weinig voor dat iemand die de ziekte niet heeft toch een positieve uitslag krijgt.
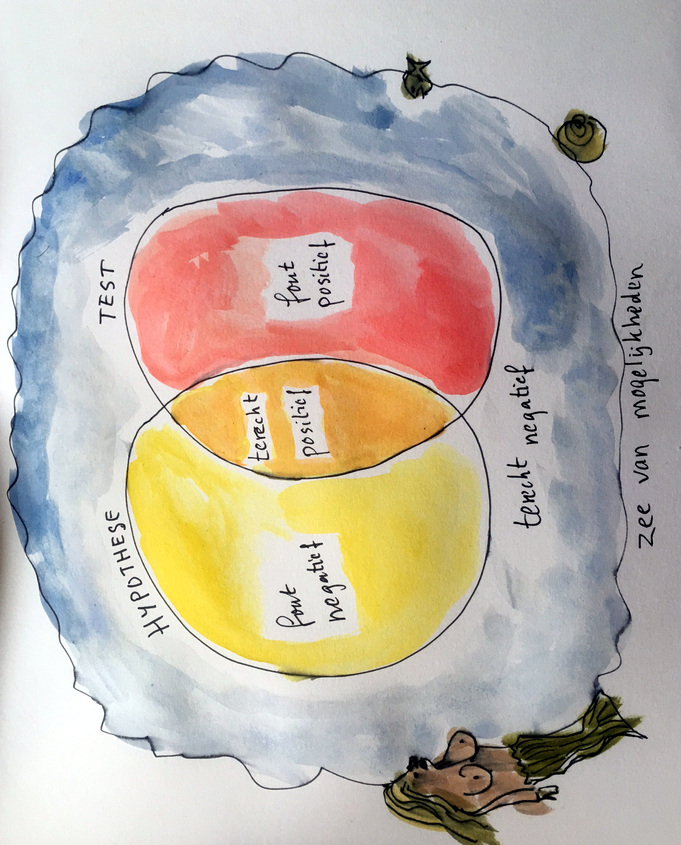
In het plaatje helemaal boven zijn de verschillende mogelijkheden te zien. In een ideale situatie zouden het rode en het gele gebied elkaar precies dekken. De test-uitslag komt dan precies overeen met datgene waarvoor wordt getest.
Fout negatieve uitslagen zijn problematischer dan fout positieve uitslagen, dus gevoeligheid is belangrijker dan specificiteit. Als iemand ten onrechte een positieve uitslag krijgt wordt dat immers in het vervolgtraject wel duidelijk. Maar als iemand ten onrechte een negatieve uitslag krijgt wordt die persoon misschien ten onrechte minder voorzichtig.
In laboratorium situaties is de PCR test zowel zeer gevoelig als zeer specifiek, maar in de praktijk is dat een stuk minder. Zie dit Wikipedia lemma voor meer info. Ik zal er bij mijn berekeningen van uit gaan dat het percentage fout positieve uitslagen van de PCR test 2 procent is en het percentage fout negatieve uitslagen 20 procent. Deze keuze is gebaseerd op informatie die ik heb gehaald uit dit RIVM document.
Redeneren over waarschijnlijkheid
OK, ik laat me testen en de uitslag is positief. Hoe waarschijnlijk is het nu dat ik de ziekte heb? De mensen die denken dat dat nu honderd procent zeker is houden geen rekening met de mogelijkheid van fout positieve uitslagen.
Volgens de Engelse amateur wiskundige (en dominee) Thomas Bayes (1701 - 1761) kunnen we de waarschijnlijkheid dat ik de ziekte heb bij positieve testuitslag, uitrekenen op basis van de aanvankelijke waarschijnlijkheid dat ik de ziekte heb plus informatie over de betrouwbaarheid van de test.
Kijk weer naar het plaatje aan het begin. Hoe waarschijnlijk is het dat ik in het oranje gebied zit (positieve uitslag plus ziek), gegeven dat ik in het rode gebied zit (positieve testuitslag)?
De regel van Bayes
In elk geval is het zo dat de waarschijnlijkheid dat ik in het oranje gebied zit (zowel ziek als positief getest) wordt gegeven door:
\(P(H \cap T) = P(H \mid T) P (T)\).
Uitleg:
\(P (H \cap T)\) staat voor ‘de waarschijnlijkheid van zowel \(H\) als \(T\)’,
\(P (H \mid T)\) staat voor ‘de waarschijnlijkheid van \(H\), gegeven dat \(T\) het geval is’,
\(P(T)\) staat voor `de waarschijnlijkheid van \(T\)’,
\(P(H \mid T) P (T)\) staat voor het product van de waarschijnlijkheden \(P(H \mid T)\) en \(P (T)\).
Denk bij waarschijnlijkheden weer aan breuken tussen 0 en 1.
Maar \(H\cap T\) is hetzelfde als \(T \cap H\), dus er geldt ook:
\(P(H \cap T) = P(T \cap H) = P(T \mid H) P (H)\).
Dit geeft de volgende belangrijke gelijkheid:
\(P(H \mid T) P (T) = P(T \mid H) P (H)\).
Als we aannemen dat \(P(T)\) groter is dan 0 mogen we aan beide kanten door \(P(T)\) delen. Zo krijgen we de beroemde regel van Bayes:
\(P (H \mid T) = \frac{P(T \mid H) P(H)}{P(T)}\).
De regel zegt: de waarschijnlijkheid van ziek zijn gegeven een positieve test is gelijk aan de waarschijnlijkheid van een positieve test gegeven ziek zijn maal de waarschijnlijkheid van ziek zijn binnen de zee van alle mogelijkheden. In dit geval wordt de zee van alle mogelijkheden gegeven door het deel van de bevolking dat zich laat testen. Het delen door \(P(T)\) dient om te normaliseren, dat wil zeggen om ervoor te zorgen dat onze waarschijnlijkheden in het interval tussen 0 en 1 blijven.
Het belang van de prior
De waarschijnlijkheid \(P(H)\) wordt wel de prior genoemd. Maar hoe kan ik die weten voordat ik me laat testen? Antwoord: de prior kun je inderdaad niet precies weten, maar je kunt wel een goede schatting maken. Als ik me laat testen kan dat allerlei redenen hebben. Het zou bij voorbeeld kunnen dat ik me niet lekker voel en dat ik niet opknap van het doornemen van de lijst van covid-19 verschijnselen op internet. Maar het kan ook dat een vriendin van onze dochter zojuist te horen heeft gekregen dat ze covid-19 heeft en dat ik niet opknap van wat ik weet over hoeveel afstand onze dochter houdt tot haar vriendinnen. Eigenlijk doet dat er allemaal niet zoveel toe. Wat ertoe doet is dat ik me, met mijn besluit om me te laten testen, plaats in de categorie van mensen die dat ook doen. Dus ik kan afgaan op de GGD informatie. Het blijkt dat op dit moment (afgerond) 11 procent van de mensen die zich laten testen een positieve uitslag krijgt. Dat is dus mijn prior.
Waarschijnlijkheid van ziek zijn bij positieve testuitslag
\(P(T \mid H)\) weet ik, want dat is de waarschijnlijkheid dat mijn positieve testuitslag correct is. Als de PCR test 20 procent false negatives geeft is dit dus 80 procent, ofwel \(0.8\) (met decimale punt in plaats van decimale komma).
En \(P(T)\) weten we ook, want daarvoor geldt:
\(P(T) = P(T \mid H) P(H) + P(T \mid \overline{H}) P(\overline{H})\).
Hierbij staat \(\overline{H}\) voor “de ziekte niet hebben”. Hier staat dus: de waarschijnlijkheid van een positieve test wordt gegeven door de som van de waarschijnlijkheid van een terecht positieve uitslag als je de ziekte hebt en de waarschijnlijkheid van een fout positieve uitslag als je de ziekte niet hebt.
Uitrekenen geeft:
\(P(H \mid T) = \frac{0.8 * 0.11}{0.8 * 0.11 + 0.02 * 0.89} \approx 0.83\).
Gegeven wat we weten over de prior en over de betrouwbaarheid van de PCR test is de waarschijnlijkheid dat ik de ziekte heb bij een positieve testuitslag iets meer dan 83 procent.
Wat testen ons vertelt
Uitleggen hoe iets zit is gemakkelijker dan onzin weerleggen. “Als je meer test krijg je meer gevallen, dus je kunt beter minder testen.” Dit is veelgehoorde Trumpiaanse onzin. Het verwaarloost het onderscheid tussen hoe het is aan de ene kant (de werkelijkheid) en wat wij kunnen weten over hoe het is aan de andere kant (onze kennis of onwetendheid over de werkelijkheid).
Testen creëert de ziekte niet. Er komen door te testen geen gevallen bij. Testen kan wel onzekerheid genereren. Dit gebeurt als we een test gebruiken die niet specifiek genoeg is, want dan zullen we te maken krijgen met veel fout positieve uitslagen. Gelukkig is de PCR test voor covid-19 behoorlijk specifiek. Als je het plaatje aan het begin van deze blog snapt weet je nu hoe dit allemaal zit.