Twijfelen aan de Werkelijkheid (7)

Bewijs, waarheid, zekerheid
De Griekse wiskundigen uit de Oudheid waren de uitvinders van het wiskundig bewijs. Een bewijs in de wiskunde toont aan dat een bewering volgens heel precieze regels kan worden afgeleid uit axioma’s. Als we de waarheid van de axioma’s inzien dan moeten de beweringen waarvoor we een bewijs hebben ook waar zijn.
Met het begrip bewijs vonden de Grieken de weg naar absolute zekerheid wanneer het ging om zaken die te maken hadden met vormen (lijnen, cirkels, driehoeken, …) en met getalsverhoudingen. De Grieken hadden daarmee een methode gevonden om inzicht in de werkelijkheid te krijgen waar niet aan te twijfelen viel. Het Nederlandse woord wiskunde danken we aan Simon Stevin (1548 - 1620). Wiskunde is de kunst van het denken over zaken die gewis zijn.
Later ontstond er toch weer twijfel over de vraag of de meetkundige axioma’s van Euclides de werkelijkheid correct beschrijven, maar dit terzijde, want daar hebben we het hier al over gehad.
Bewijzen snappen en bewijzen vinden
De Griekse filosoof Aristoteles merkte op dat er een immens verschil was tussen de volgende twee activiteiten:
een gegeven bewijs begrijpen,
zelf een bewijs produceren.
Wanneer iemand hem een wiskundige uitspraak voorlegde met een bewijs erbij, dan kon hij vrij gemakkelijk de stappen van dat bewijs nagaan en zo zichzelf ervan overtuigen dat dat bewijs klopte, en dat de bewering dus waar was. Maar wanneer iemand hem diezelfde uitspraak gaf zonder bewijs, dan kostte het hem meestal de grootste moeite om in te zien dat de bewering waar was. In veel gevallen slaagde hij er dan niet in zelf een bewijs te vinden. Goed-gestructureerde bewijzen begrijpen en nagaan of ze kloppen is relatief gemakkelijk. Zelf bewijzen produceren is veel moeilijker.
Illustratie: Tangram
We kunnen dit illustreren met een analogie. Ziehier een doe-het-zelf instructie om een Tangram spel te fabriceren door een vierkant vel papier in stukken te knippen volgens het lijnenpatroon. Dit geeft twee grote driehoeken, een middelgrote driehoek, twee kleine driehoeken, een vierkant en een wiebertje.
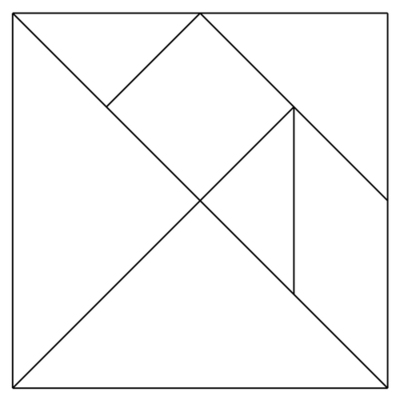
Een Tangram opgave is een figuur van een bepaalde vorm. De opgave is om deze vorm te construeren door de zeven Tangram vormen te combineren. Hier is een voorbeeld.

En hier is de oplossing:
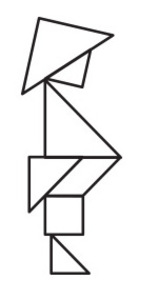
Het is gemakkelijk om na te gaan dat de oplossing precies de zeven Tangram vormen gebruikt, en dat het dus een correcte oplossing is. Maar zelf zo’n oplossing vinden is vaak een stuk moeilijker. Geef maar eens iemand de zeven Tangram vormen, met de opdracht het oorspronkelijke vierkant waaruit de stukken geknipt zijn te reconstrueren.
Hoe ontstaat plotseling inzicht?
Op dezelfde manier kunnen we de ervaring hebben van ineens de oplossing zien van een raadsel. Het hoeft niets met wiskunde te maken te hebben. We verplaatsen ons in iemand en we hebben plotseling door waarom die persoon boos op ons is. We breken ons het hoofd over een cryptogram en ineens schiet ons het woord te binnen dat voldoet aan de omschrijving.
Hier is een ander voorbeeld, uit de tijd dat ik nog op het CWI (Centrum voor Wiskunde en Informatica) werkte. In die tijd was er naast het Amolf gebouw op het Science Park, vlakbij het CWI, een parkeerterrein. Intussen staat daar een nieuw gebouw, maar destijds zag het er zo uit:

Op de foto is alleen een klein stukje van de parkeerplaats zichtbaar. Op werkdagen fietste ik tweemaal daags langs dit gebouw, heen naar het CWI, en weer terug naar huis. Bij het naar huis fietsen, zo rond een uur of zeven ’s avonds, zag ik dan altijd een paar auto’s vlakbij het gebouw en een behoorlijk aantal auto’s op de parkeerplekken het verst van het gebouw af. Dat was elke avond zo. Hoe kwam dit?
Bij dit soort zaken is het interessant om te kijken naar hoe onze geest werkt. Eerst rijd je er langs en er valt je niets op. Op zeker moment zie je regelmaat maar schenk je er geen aandacht aan. En dan, ineens, snap je het. De Amolf onderzoekers hebben flexibele werktijden. De vroege vogels zetten hun auto’s op een lege parkeerplaats, vlakbij het gebouw. De mensen die pas rond twaalven komen aankakken kunnen alleen nog verderop een plekje voor hun auto vinden. Dat zijn ook de mensen die ’s avonds het laatst vertrekken. Ze zijn er dus nog om zeven uur ’s avonds, en daarom zie ik hun auto’s aan de buitenkant van het parkeerterrein staan terwijl de rest van het terrein nagenoeg verlaten is.
Het aardige is dat je er, op het moment dat je zo’n inzicht krijgt, vrijwel zeker van kunt zijn dat het klopt. Dit is het gevoel van ‘iets door hebben’. Je snapt het pas als je het door hebt, om met de Nederlandse voetbalfilosoof Johan Cruyff (1947 - 2016) te spreken.
In alle eenvoud
Hier is een ander voorbeeld, uit het (zeer aanbevolen) boekje Boeddhisme, in alle eenvoud, van Steve Hagen.

Sommige mensen zien meteen waar dit een plaatje van is, maar de meeste mensen niet. Als je bij die laatste categorie hoort is het volgende interessant om te doen. Blijf rustig naar het plaatje kijken. Als je geluk hebt komt er dan een moment waarop je het ineens ziet. Observeer nu wat er op dat moment in je geest gebeurt. Let met name op het gevoel van absolute zekerheid dat je het nu goed ziet.
De auteur van het boek met dit plaatje vergelijkt de ervaring van plotseling zien wat er op het plaatje staat met het gevoel van plotseling zien waar het in ons leven om gaat.
En toch: je kunt een gevoel van diep inzicht in de werkelijkheid hebben terwijl je er volkomen naast zit. Ons gevoel van zekerheid kan ons altijd misleiden. Een heel klein beetje twijfel aan ons inzicht in de werkelijkheid is daarom nooit verkeerd.